Каждая волна подразделяется на меньшие
Каждая волна подразделяется на меньшие волны, которые в свою очередь также разбиваются на волны - еще меньшей степени. Естественно, отсюда следует, что каждая из волн фактически является частью большей, следующей в волновой иерархии. Пример такой иерархии представлен на рис. 13.2. Две самые крупные волны - (1)и(2) подразделяются на восемь меньших, которые в свою очередь могут быть далее разбиты на тридцать четыре еще меньшие волны. Эти две большие волны - (J)11® представляют собой лишь первые две волны, входящие в состав еще более значительной пятиволновой восходящей тенденции. За ними должна последовать волна (з), относящяяся к тому же иерархическому уровню. Тридцать четыре волны, изображенные на рис. 13.2, при переходе на одну степень вниз подразделяются уже на сто сорок четыре (см. рис. 13.3).
Числа 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, которые довольно часто встречаются на страницах этой книги, не случайны. Они входят в так называемую числовую последовательность Фибоначчи, которая служит математической основой теории волн Эллиота. К этой теме мы еще вернемся, а пока посмотрите на примеры (рис. 13.1-13.3), демонстрирующие весьма важную особенность волн. На сколько меньших волн может быть разбита данная волна (три или пять), зависит от направления большей волны, частью которой она является. Так, волны (1), (3) и (5) (рис. 13.2) подразделяются на пять волн каждая, поскольку волна большей степени, волна (l) - восходящая. Поскольку волны (2) и (4) идут в противоположном тенденции направлении, они разбиваются только на три волны меньшей степени. Посмотрите внимательнее на корректирующие волны (а), (Ь), (с); они составляют корректирующую волну (2) (большей степени). Обратите внимание, что две опускающиеся волны - (а) и (с) - подразделяются на пять меньших волн каждая, поскольку идут в том же направлении, что и большая по степени волна (2). Волна (с), наоборот, состоит всего из трех волн, поскольку идет в направлении, противоположном следующей более крупной волне (2).
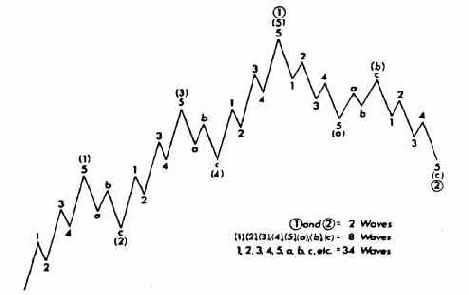
Рис. 13.2.
